类型
C++的类型分为基础类型和复合类型。
基础类型
基础类型包含一下类型
void
void:表示空,比如表示函数什么都不返回。
nullptr_t
nullptr_t: 也就是空指针字面变量(nullptr)的类型。它的特殊之处在于这个类型本身并不是一个普通指针类型,也不是一个指向成员的指针类型。它的值(nullptr)是一个null pointer constants,可以隐式转换为任何指针或者指向成员的指针类型。
算数类型
bool类型
c++里面的bool类型跟其它语言一样,用来表达true和false
字符类型:
窄字符类型有char, signed char, unsigned char。c++20又引入了char8_t。char类型一直以来的问题就是有的平台是有符号数数,有的平台是无符号数。X86 GNU/Linux和Windows使用的是signed char,而PowerPC和ARM处理器一般都是使用unsigned char作为char。char8_t引入指定了使用的是unsigned char,但是它并不是unsigned char的别名,而是一个新的类型。它用来保证一定可以装下utf-8的字符。
宽字符类型有wchar_t,c++11中引入了char16_t, char32_t。需要注意的是char16_t是用来存储UTF-16的字符,它是uint_least16_t的别名。也就是说:1. 它保证是无符号的;2. 至少有16比特,但是不一定,可能有20比特,也可能有32比特。char32_t也是一样的,是uint_least32_t的别名,用来存储UTF-32的字符。
无符号整数
无符号整数:unsigned short int, unsigned int, unsigned long int。从C99(C语言1999标准),头文件stdint.h引入了如下的无符号类型:
uint8_t: 精确的8比特无符号数uint16_t: 精确的16比特无符号数uint32_t: 精确的32比特无符号数uint64_t: 精确的64比特无符号数
还有如下fast系列
uint_fast8_t:至少8比特的最快的无符号整数类型uint_fast16_t:至少16比特的最快的无符号整数类型uint_fast32_t:至少32比特的最快的无符号整数类型uint_fast64_t:至少64比特的最快的无符号整数类型
以及最小内存系列
uint_least8_t:至少8比特的无符号整数类型uint_least16_t:至少16比特的无符号整数类型uint_least32_t:至少32比特的无符号整数类型uint_least64_t:至少64比特的无符号整数类型
个人理解是fast系列偏向速度,least系列偏向内存消耗。比如寄存器至少都是16位的,那么uint_fast8_t选择uint16_t应该就比uint8_t要好。而对于uint_least8_t就刚好相反,它更看中存储大小,选择uint8_t更好。
fast和least系列大家使用不多。日常编程建议使用精确大小的无符号类型,这样确定知道大小。因为c++标准是没有规定具体大小的,只是规定了signed char, unsigned char是至少有8比特;short int, unsigned short int是至少有16比特;int, unsigned int至少有16比特;long int, unsigned long int至少有32比特;long long int, unsigned long long int至少有64比特。所以我们只知道至少多少比特,并不知道具体多少比特,如果我们的程序是需要跨平台的,就可能在不同平台出现不一致的表现。
对于一个二进制序列b_n b_{n-1} b_{n-1} b_{n-3} \cdots b_b b_0,其表达的十进制值为:
比如一个3比特的二进制,我们有
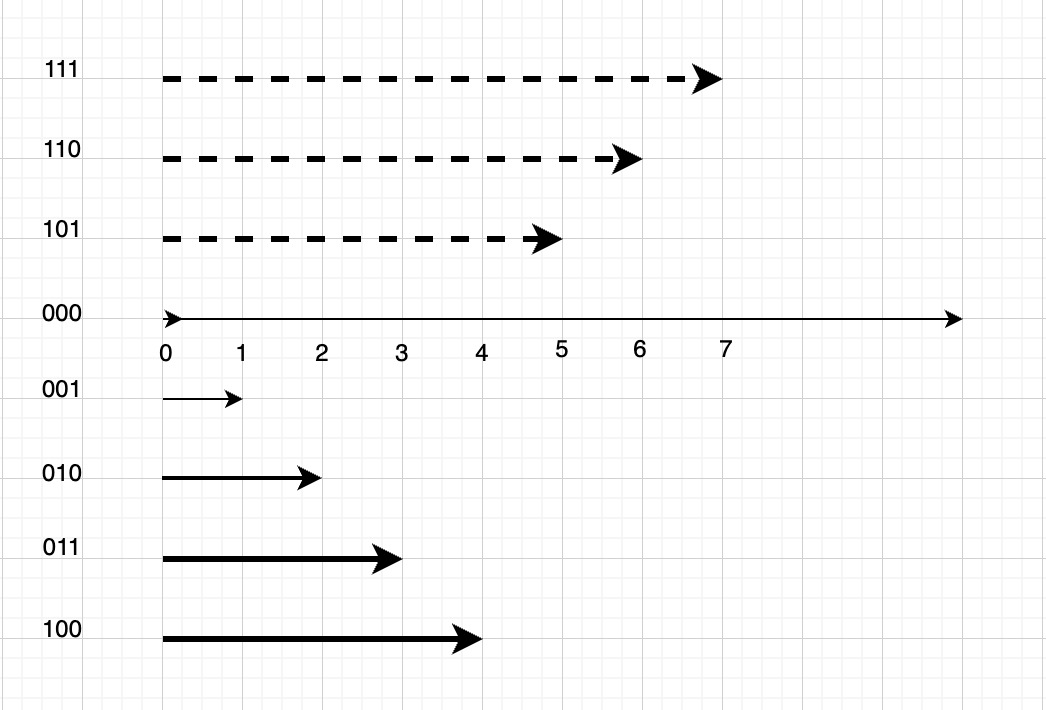
有符号整数
有符号整数:short int, int, long int。从C99(C语言1999标准),头文件stdint.h引入了如下的无符号类型:
int8_t: 精确的8比特有符号数int16_t: 精确的16比特有符号数int32_t: 精确的32比特有符号数int64_t: 精确的64比特有符号数
还有如下fast系列
int_fast8_t:至少8比特的最快的有符号整数类型int_fast16_t:至少16比特的最快的有符号整数类型int_fast32_t:至少32比特的最快的有符号整数类型int_fast64_t:至少64比特的最快的有符号整数类型
以及最小内存系列
int_least8_t:至少8比特的有符号整数类型int_least16_t:至少16比特的有符号整数类型int_least32_t:至少32比特的有符号整数类型int_least64_t:至少64比特的有符号整数类型
n比特的有符号整数中我们用最高比特用来表达-2^{n-1},其它比特按照无符号整数进行表达,表达的十进制为
3比特的的表达我们可以表示如下图:
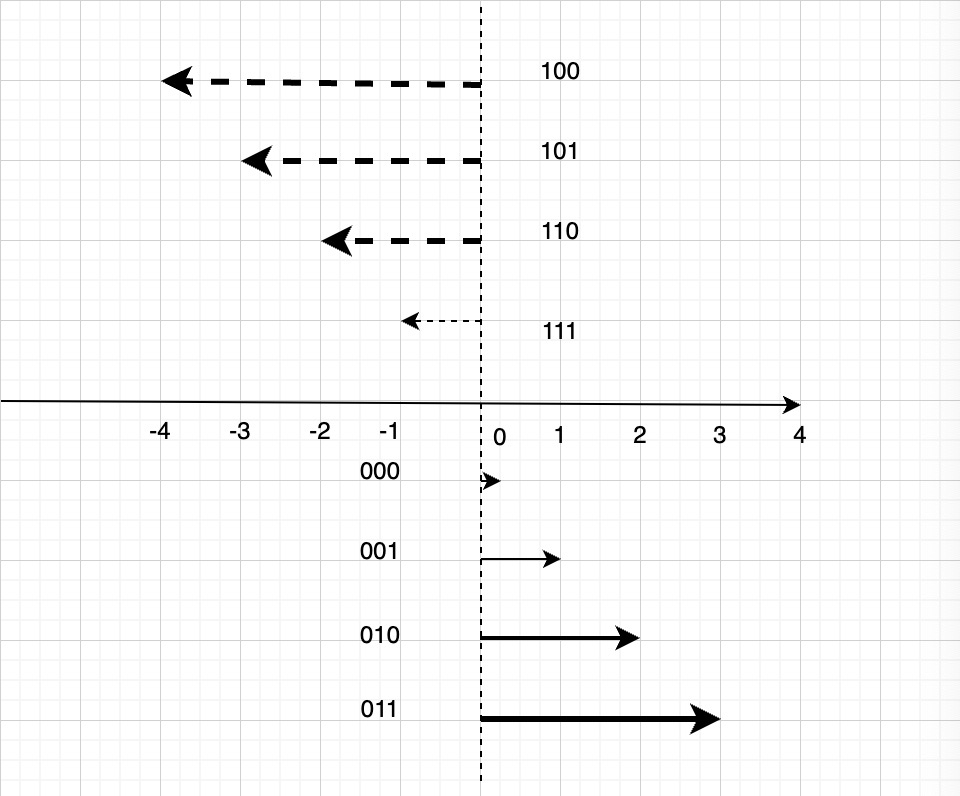
纯粹从2进制比特来看,对于一个有符号整数,-x的表示(x>0)是x的二进制取反加上1。
比如上图中2的二进制为010, -2的二进制110,恰好是010取反得到的101加上1得到。
浮点数类型
浮点类型包括float, double, long double。都是使用IEEE 754标准表达。表达方式为:
| sign | exponent | fractional | 浮点数的二进制表示分为三个部分
1位表示符号(记做s):0表示正数,1表示负数;
k位表示指数(记做E):(e_{k−1}e_{k−2}e_{k−3}...e_0)_2
n位表示小数部分(记做M):(m_1m_2m_3...m_n)_2=m_1×2^{−1}+m_2×2^{−2}+⋯+m_n×2^{−n}
浮点数就表示为(−1)^s×M×2^E。
对于32位的浮点数,k=8, n=23;对于64位的浮点数,k=11,n=52。
首先根据表示指数的位数我们设置一个偏移量Bias(Bias=2^{k−1}−1)。这个偏移量来干什么呢?无符号的k比特的二进制数是一个大于等于0的十进制数,是没有办法表达负数的。而我们其实是需要负数来表示小于1的数的。所以我们设置一个偏移量来干这个事情。
对于浮点的指数部分,在不考虑Bias的情况下,k个比特能够表达0到2^k−1的数字,但是我们把全1用来表达无穷大,把全0用来表示小于0的数,所以还剩下1到2^k−2部分。
表达分为三种:
当指数不是全0和全1的时候,我们称为normalized浮点数表示,指数E=e−Bias,其中e是(e_{k−1}e_{k−2}e_{k−3}...e_0)表达的无符号数。由于我们使用了全0的指数来表达绝对值小于1的数,我们认为这部分数的小数部分是M=1+f,其中f是(m_1m_2m_3...m_n)_2表示的小数部分,0\le f \le 1, 1\le 1+f \le 2。
当指数全部都是0的时候,我们称为denormalized浮点表示,指数E=1−Bias,小数部分为M=f。这里需要注意的是当f的每个数位都为0的时候,f为0。但是s为0的时候表示+0,为1的时候表示-0。也就是IEEE 754B标准中0不唯一。
当指数全部为1的时候,我们表示无穷大。s为0的时候表示+\infty,为1的时候表示-\infty。
考虑一个6比特的浮点数,其中我们使用1比特表示符号,3比特表示指数,2个比特表示小数。\text{Bias}=2^2−1=3。
首先我们来看normalized浮点表示: 指数E_{max}=2^3−2−Bias=3, E_{min}=1−3=−2。
而对于denormalized类型浮点: 指数E_{max}=1−Bias=1−3=−2
我们打印出除了无穷大之外的所有大于等于0的数如下表,小于0的部分只需要前面加上负号。
对于32位的浮点数,使用了8位来表示指数,那么Bias=27−1=127
normalized表示的时候, Emax=28−2−Bias=254−127=127, Emin=1−127=−126;
denormalized表示的时候, E=1−127=−126
也就是说:
大于0的最大的浮点数的比特为0 11111110 11111111111111111111111
大于0的次大的浮点数的比特为0 11111110 11111111111111111111110
大于0的次小的浮点数的比特为0 00000000 00000000000000000000010
大于0的最小的浮点数的比特为0 00000000 00000000000000000000001
结语
亲爱的小伙伴,看您通过本文了解了多少呢?如果想了解更多,可以通过公众号和知乎进行了解。
公众号:探知轩





评论区